CNN?
Convolutional Neuraal Network(합성곱신경망)이란 인공신경망의 다양한 구조 중 입력(X)을 일정하게 나눠 (X1 X2 X3 X4 …) Conv 계층을 만들고, 이 계층에 어떤 Weight값을 할당해 활성함수로 연산한 후 일반적인 신경망으로 전달하는 구조의 신경망이 Convolutional Neural Network의 아이디어이다.
Conv 계층?
32x32 사이즈의 이미지 파일이 있다고 하자. 이 이미지는 RGB의 3색으로 이루어져 있기 때문에,
32x32x3의 이미지라고 할 수 있다.
이 이미지를 부분적으로 처리하기 위해 하나의 작은 구역 Filter를 만든다고 생각해보자.
이 Filter의 크기를 5x5x3이라고 생각해보자.
이 Filter는 원래의 이미지에서 5x5에 해당하는 영역에서 하나의 수를 뽑아내는 역할을 한다.
이 하나의 값은 \(Wx+b\)의 꼴로 구해지며, x와 W는 각각 5x5x3개 존재한다. 이제 이 값에 활성화 함수 ReLU등을 적용해 응용할 수 있다.
이제 똑같은 필터, 똑같은 w를 옮기며 원 이미지의 다른 부분을 살펴보기 위해 필터를 이동시키며 각각의 위치에 따른 값을 구해야 한다.
7x7의 이미지에서 3x3의 필터를 한 칸씩 움직일 때 확인할 수 있는 값은 5x5의 출력이다. 여기서 한 칸은 stride 크기가 1이라고도 맗한다. 만약 7x7의 이미지에서 3x3 필터를 2칸씩 움직인다면 3x3의 출력을 얻을 수 있다.
출력의 크기는 다음과 같이 구할 수 있다.
\((N - Filter) / stride + 1\)
e.g. N=8, Filter=5:
stride 1 => 3 / 1 + 1 = 4
stride 2 => 3 / 2 + 1 = 2.5 (할 수 없음)
stride 3 => 3 / 3 + 1 = 2
다만 저렇게 Filter를 적용해서 stride만큼 이동해서 output을 추출하면 입력값보다 출력값이 줄어든다. 따라서 똑같은 수의 출력을 갖기 위해 필터를 씌울 이미지에 0이 placeholder로 들어간 테두리(padding)를 추가하는 기법을 사용한다. 예를 들어 7x7의 입력에 1픽셀의 테두리를 추가하면 출력은 (9-3)/1+1 = 7으로 출력값에 손실이 없어진다. 패딩기법을 사용하는 이유는 크게 두 가지로 하나는 이미지가 급격하게 작아지는 것을 방지하기 위함이고 다른 하나는 이미지의 가장자리를 네트워크에 전하기 위해서라고 볼 수 있다. 입력과 출력의 수가 같아질 만큼 패딩을 추가하는 것이 일반적이다.
32x32x3의 이미지를 5x5x3의 필터를 이용해 돌면 하나의 출력 레이어가 생긴다. 마찬가지로 필터의 숫자를 늘려 원 이미지를 훑게 되면 그만큼의 레이어가 생긴다. 각각의 필터는 weight가 달라 나오는 값은 조금 다를 수 있다.
만약 5x5x3 사이즈의 필터 6개를 Convolutional Layer에 적용시키게 되면 깊이 6, 패딩을 하지 않을 경우 28x28의 크기를 가진 activation map이 생긴다.
이런 Convolution layer를 여러 개 만들 수도 있다.
예를 들어 깊이가 6인 5x5x3의 필터로 만든 레이어(Activation map)에 convolution layer를 적용한다고 치자.
이 Convolution layer는 5x5x6의 filter 10개로 이루어져 있고 stride 1 기준 크기는 24x24 일 것이다.
각 레이어에 대한 Weight의 수는 가로x세로x두께x개수로 구하면 된다. 이 Weight 값은 Random한 방법으로 초기화해서 구한다.
Pooling layer
Conv layer의 사이즈를 줄이는 과정을 sampling, pooling이라고 한다. Activation map에서 한 layer를 뽑아서 pooling하는 과정을 반복해 pooling된 각 레이어들을 쌓아 Activation map을 이룬다.
MAX pooling
4x4의 이미지에 2x2의 필터로 stride 2씩 움직이면 출력은 2x2가 된다. 2x2로 사이즈를 줄이기 위한 방법으로 stride 2씩 움직이는 각 구간 안의 숫자를 다 더해 평균을 내는 방법, 각 구간 안에서 가장 작은 값, 가장 큰 값을 고르는 방법 등이 있다. 가장 많이 사용되는 방법은 필터에서 가장 큰 값을 고르는 MAX Pooling이다.
1 1 2 4
5 6 7 8 > 6 8
3 2 1 0 > 3 4
1 2 3 4
Filter와 Stride의 갯수에 따라 Pooling된 출력값의 크기가 정해질 것이다.
Fully Connected layer
CONV 기법과 Pooling 기법을 이용해 다양한 모델을 설계할 수 있다.
e.g.
CONV - ReLU - CONV - ReLU - POOL - CONV -ReLU - CONV -ReLU - POOL - CONV - ReLu
CONV - ReLU - POOL - Fully Connected Network - Softmax Classify
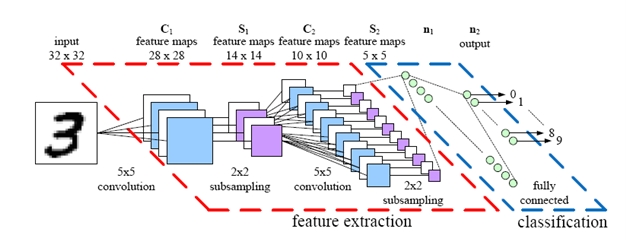
Case Study
AlexNet
입력: 227 x 227 x 3 이미지
첫 layer (CONV1): 96 11x11x3 filters applied at stride 4
=>
출력 볼륨 55x55x96
파라미터: 11x11x3x96=35K
두번째 layer (POOL1): 3x3 filters applied at stride 2
=>
출력 볼륨 27x27x96
파라미터: 0
CONV1
POOL1
…
Full (simplified) AlexNet architecture:
[227x227x3] INPUT
[55x55x96] CONV1: 96 11x11 filters at stride 4, pad 0
[27x27x96] MAX POOL1: 3x3 filters at stride 2
[27x27x96] NORM1: Normalization layer
[27x27x256] CONV2: 256 5x5 filters at stride 1, pad 2
[13x13x256] MAX POOL2: 3x3 filters at stride 2
[13x13x256] NORM2: Normalization layer
[13x13x384] CONV3: 384 3x3 filters at stride 1, pad 1
[13x13x384] CONV4: 384 3x3 filters at stride 1, pad 1
[13x13x256] CONV5: 256 3x3 filters at stride 1, pad 1
[6x6x256] MAX POOL3: 3x3 filters at stride 2
[4096] FC6: 4096 neurons
[4096] FC7: 4096 neurons
[1000] FC8: 1000 neurons (class scores)
Details/Retrospectives:
- first use of ReLU
- used Norm layers (not common anymore)
- heavy data augmentation
- dropout 0.5
- batch size 128
- SGD Momentum 0.9
- Learning rate 1e-2, reduced by 10
manually when val accuracy plateaus
- L2 weight decay 5e-4
- 7 CNN ensemble: 18.2% -> 15.4%
CNN의 기본 아이디어만 가지고도 엄청나게 다양한 네트워크를 구성할 수 있다.
MNIST Challenge
우리의 모델
INPUT : 28x28x1
CONV1: 1 stride, padding = same
POOL1: 2 strides, padding = same
DROPOUT 0.8
CONV2: 1 stride, padding = same
POOL2: 2 strides, padding = same
DROPOUT 0.8
CONV3: 1 stride, padding = same
POOL3: 2 strides, padding = same
DROPOUT 0.8
Fully Connected Net
l4 = tf.nn.relu(tf.matmul(l3, w4))
DROPOUT 0.5
OUTPUT : pyx = tf.matmul(l4, w_o)
#---------------------------------
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
batch_size = 128
test_size = 256
def init_weights(shape):
return tf.Variable(tf.random_normal(shape,stddev=0.01))
def model(X, w, w2, w3, w4, w_o, p_keep_conv, p_keep_hidden):
l1a = tf.nn.relu(tf.nn.conv2d(X, w, # l1a shape=(?, 28, 28, 32)
strides=[1, 1, 1, 1], padding='SAME'))
l1 = tf.nn.max_pool(l1a, ksize=[1, 2, 2, 1], # l1 shape=(?, 14, 14, 32)
strides=[1, 2, 2, 1], padding='SAME')
l1 = tf.nn.dropout(l1, p_keep_conv)
l2a = tf.nn.relu(tf.nn.conv2d(l1, w2, # l2a shape=(?, 14, 14, 64)
strides=[1, 1, 1, 1], padding='SAME'))
l2 = tf.nn.max_pool(l2a, ksize=[1, 2, 2, 1], # l2 shape=(?, 7, 7, 64)
strides=[1, 2, 2, 1], padding='SAME')
l2 = tf.nn.dropout(l2, p_keep_conv)
l3a = tf.nn.relu(tf.nn.conv2d(l2, w3, # l3a shape=(?, 7, 7, 128)
strides=[1, 1, 1, 1], padding='SAME'))
l3 = tf.nn.max_pool(l3a, ksize=[1, 2, 2, 1], # l3 shape=(?, 4, 4, 128)
strides=[1, 2, 2, 1], padding='SAME')
l3 = tf.reshape(l3, [-1, w4.get_shape().as_list()[0]]) # reshape to (?, 2048)
l3 = tf.nn.dropout(l3, p_keep_conv)
l4 = tf.nn.relu(tf.matmul(l3, w4))
l4 = tf.nn.dropout(l4, p_keep_hidden)
pyx = tf.matmul(l4, w_o)
return pyx
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels
trX = trX.reshape(-1, 28, 28, 1)
teX = teX.reshape(-1, 28, 28, 1)
X = tf.placeholder("float", [None, 28, 28, 1])
Y = tf.placeholder("float", [None, 10])
w = init_weights([3,3,1,32])
w2 = init_weights([3,3,32,64])
w3 = init_weights([3,3,64,128])
w4 = init_weights([128*4*4, 625])
w_o = init_weights([625,10])
p_keep_conv = tf.placeholder("float")
p_keep_hidden = tf.placeholder("float")
py_x = model(X, w, w2, w3, w4, w_o, p_keep_conv, p_keep_hidden)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=py_x, labels=Y))
train_op = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost)
predict_op = tf.argmax(py_x, 1)
with tf.Session() as sess:
tf.global_variables_initializer().run()
for i in range(15):
training_batch = zip(range(0, len(trX), batch_size),
range(batch_size, len(trX)+1, batch_size))
for start, end in training_batch:
sess.run(train_op, feed_dict={X: trX[start:end], Y: trY[start:end],
p_keep_conv: 0.8, p_keep_hidden: 0.5})
test_indices = np.arange(len(teX))
np.random.shuffle(test_indices)
test_indices = test_indices[0:test_size]
print(i, np.mean(np.argmax(teY[test_indices], axis=1) ==
sess.run(predict_op, feed_dict={X: teX[test_indices],
Y: teY[test_indices],
p_keep_conv: 1.0,
p_keep_hidden: 1.0})))
0 0.96875
1 0.98828125
2 0.98046875
3 0.984375
4 0.98828125
5 0.9921875
6 0.9921875
7 0.9765625
8 1.0
9 0.99609375
10 0.9921875
11 0.9921875
12 0.98828125
13 0.9921875
14 0.99609375
15 1.0