로지스틱 회귀(Logistic Regression)

로지스틱 회귀란 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법이다.
로지스틱 회귀의 목적은 일반 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적 함수로 나타내 향후 예측 모델에 사용하는 것이다. 이는 독립 변수의 선형 결합으로 종속 변수를 설명한다는 관점에서 선형 회귀 분석과 비슷하다. 그러나 로지스틱 회귀는 선형 회귀 분석과 달리 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류(Classification) 기법으로도 볼 수 있다. 로지스틱 회귀는 주로 종속변수가 이항형인 문제를 지칭할 때 쓰인다. 두 개 이상의 범주를 다루는 경우 다항 로지스틱 회귀(multinomial logistic regression)이라고 하며 복수의 범주이며 순서가 존재하면 서수 로지스틱 회귀(ordinal logistic regression)이라고 한다.

• 본문의 일부는 Data Science from scratch(밑바닥부터 시작하는 데이터 과학)을 참고했습니다.
• 본문의 소스코드의 일부는 Joel Grus의 Github에서 Unlicensed 라이선스로 배포되고 있습니다.

문제

회사원의 경력, 소득, 유료 계정 등록 여부 데이터를 갖고 모델을 만들고자 한다. 찾고자 하는 종속 변수(dependent variable)는 유료 계정 등록 여부이며, 이는 0(아니다)에서 1(맞다)의 값을 가진다. 선형 회귀 분석을 통해서도 독립 변수와 종속 변수를 이용해 어떤 결과값을 찾아낼 순 있지만, 몇 가지 문제점이 있다.

• 예측값이 정확히 0 또는 1이거나 확률로 간주할 수 있도록 0이나 1 사이의 값이 나와야 어떤 클래스에 대한 예측인지 알 수 있다. 그런데 선형 회귀 모델의 결과값은 아주 큰 양수값 또는 음수값일 수 있어서 해석이 어렵다.
• 선형 회귀 분석은 오류값(error)이 변수들과 아무런 상관 관계가 없다고 가정한다. 하지만 만약 선형 회귀 모델을 통해 ‘경력’이라는 항목의 계수가 양수여서 경력이 늘어날 수록 유료 계정을 등록할 가능성이 많다고 하면, 사용자의 경력이 아주 길 경우 모델은 아주 큰 예측값을 보여줄 것이다. 그러나 y의 최대치는 1이라서 아주 큰 예측값은 큰 음의 오류값을 뜻한다. (변수들과 오류값에 상관관계가 있다.) 이 경우 \(\beta\)에 대한 추정이 상당히 편향돼있다.

이렇게 하는 대신 x_i와 beta의 내적 값이 크면 예측값이 1에 가깝고 작으면 0에 가깝도록 설정할 수 있다. 이는 예측값에 특별한 함수를 적용하면 된다.

로지스틱 함수

로지스틱 회귀 분석은 로지스틱 함수를 사용한다.

def logistic(x):
  return 1.0 / (1 + math.exp(-x))

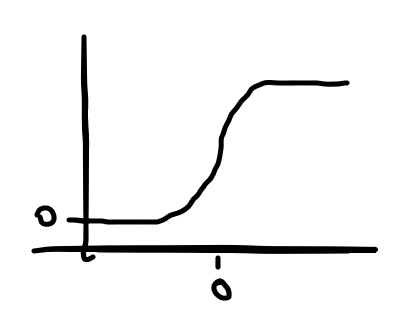
로지스틱 함수는 입력값이 커질수록 1에 가까운 출력을 하고, 입력값이 작아질수록 0에 가까운 출력을 한다.

더불어 로지스틱 함수는 다음과 같이 간단히 미분할 수 있다.

def logistic_prime(x):
  return logistic(x) * (1 - logistic(x))

이 미분식은 쓸데가 많다. 이 미분식으로 모델 학습도 시킬 수 있다.

f는 로지스틱 함수를 뜻한다.
선형 회귀 분석에서는 오차의 제곱합(sum of squared error)을 최소화해 모델 파라미터 \(\beta\)를 학습했는데 그 모델 파라미터가 결국 데이터의 likelihood를 최대화하는 값이었다.
하지만 로지스틱 회귀 분석에서 이 두 경우는 동치가 아니다. 그래서 경사 하강법을 이용해 likelihood를 최대화 시키는 방법을 사용할 수 있다. likelihood 함수와 경사를 계산하면 된다.

\(\beta\)가 주어졌을 때 \(y_i\)는 \(y_i\)는 \(f(x_i\beta)\)의 확률로 \(1, 1-f(x_i\beta)\)의 확률로 0이 되며 이애 대한 확률밀도함수는 아래와 같다.

\(y_i\)가 0이면 이 식은 이렇게 변한다.

또 \(y_i\)가 1이면 다음과 같다.

그래서 log likelihood를 최대화하는 것은 생각보다 간단하다.

log는 단조 증가 함수이고 log likelihood를 최대화하는 beta는 동시에 likelihood를 최대화하는 beta이며 그 역도 성립한다.

(코드 생략)

gradient와 likelihood함수를 구했다면 batch gradient descent나 stochastic gradient descent를 통해 모델을 학습시킬 수 있다.

적합성(Goodness of fit)

혼동행렬을 만든 후 정밀도와 재현도를 측정하자.

SVM(Support Vector Machine)

이산적인 y가 주어졌을 때 두 y의 사이를 가르는 결정 경계면 (decision boundary)를 초평면(hyperlane)이라고 부른다. 이 초평면은 likelihood를 최대화했을 때 얻을 수 있는데 분류 문제를 푸는 또 다른 방법으로 클래스를 가장 잘 분류하는 초평면을 찾는 방법이 있다. SVM은 그 중 하나로, 초평면에서 가장 가까운 점까지의 거리를 최대화하는 식으로 초평면을 찾는다.
하지만 이에는 꽤 복잡한 최적화 방법론이 필요하고 데이터를 분류할 수 있는 초평면이 존재하지 않을 수도 있다. (또 현실의 문제는 복잡하게 섥혀 있기 때문에 더 그렇다) 이 문제를 우회하기 위해서 데이터 포인트 x를 (x, x**2)로 매핑하여 2차원 공간으로 보낼 수 있다. 보통 데이터 포인트를 직접 더 높은 차원으로 매핑하기보단 커널 함수를 써서 더 높은 차원에서의 내적을 계산, 그것으로 초평면을 찾아내는 kernel trick을 사용한다.