Linear regression(선형회귀)

본문의 일부는 Data Science from scratch(밑바닥부터 시작하는 데이터 과학)을 참고했습니다.
본문의 소스코드의 일부는 Joel Grus의 Github에서 Unlicensed 라이선스로 배포되고 있습니다.

nyanye :

기술적인 용어들은 정확히 대응하는 한국어를 찾을 수가 없다는 게 아쉽다. 또 대응하는 느낌의 용어가 있다고 하더라도 오히려 원문이 더 이해하기 쉽기도 한 것 같다.

선형회귀?

Supervised Learning(교사학습)에는 크게 두 가지의 분류가 있다. Classification(분류)와 Regression(회귀) 분석.

Classification은 데이터를 통해 어떤 이산적인 결과를 도출해내기 위해 쓰인다. 예를 들어 Naive Bayes Classifier를 통해서 주어진 데이터를 통해 이 메일이 스팸 메일인가 / 아닌가를 분석하는데에 쓰였다. 물론 분류의 결과가 꼭 두 개가 아니여도 괜찮다. 스팸 유형 1번인가 스팸 유형 2번인가 스팸 유행 3번인가 이런 식의 분류가 이루어진다고 하더라도 어떤 ‘특정적’인 결과값을 원할 때 사용하는 지도학습 방법을 Classification이라고 한다. 부가적으로 Classification에서 다루는 확률을 Probability(가능성, 확률)라고 할 수 있다.

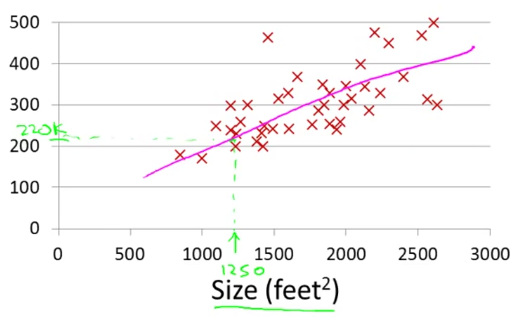
그리고 어떤 연속적인 데이터를 다루고자, 어떤 연속적인 결과 값에 도달하고자 할 때 우리가 사용하는 방법은 Regression(회귀)라고 한다. 예를 들어 집의 평수에 따른 가격을 나타내는 데이터가 있을 때 우리가 원하는 $90m^2$에 해당하는 집은 얼마일까 하는 질문에 가격을 나타내는 숫자는 ‘딱 떨어지지 않는다.’ (실수/real number)

Andrewn ng

(그림은 Coursera Andrew Ng 교수의 강의 중 등장한다. - This picture was brought from Coursera’s Andrew Ng professor’s machine learning lecture.)

우리가 가진 데이터셋은 모델을 학습시킬 training set이라고 부를 수 있다. 이 training set은 x와 y로 구분할 수 있다. x는 질문이고 y는 대답이다. 집의 평수에 따른 가격을 알고 싶다면 x는 집의 평수이고 y는 가격이다.

이러한 training set을 알고리즘에 적용시키면 Hypothesis, 가설에 해당하는 함수를 출력해준다. (주로 h라고 부른다.) 이 떄 h는 집의 평수(x)를 입력으로 받아 측정된 가격(y)을 알려주는 함수이다.

이 함수 h를 이루는 알고리즘이 선형회귀 모델이다. 회귀 모델에서(연속적인 값에서) 다루는 확률은 Likelihood(가능도, 공산, 우도)라고 할 수 있다.

모델(Simple linear regression)

\[y_i = \beta x_i + \alpha + \epsilon\]

$y_i$는 사용자 $i$가 매일 내 사이트를 이용하는 시간(분)을 의미하며, $x_i$는 사용자 $i$의 친구수를 의미한다. $\epsilon$은 모델이 고려하지 못한 어떤 요소로 인해 발생한 작은 오류를 의미한다. (아마 아주 작은)

알파와 베타가 미리 구해져 있다면, 다음 함수로 간단히 예측할 수 있다.

def predict(alpha, beta, x_i):
  return beta * x_i + alpha

알파와 베타는 어떻게 구할 수 있을까? 물론 알파와 베타의 값과 무관하게 x_i에 대한 결과는 예측이 가능하다. 실제 출력값 y_i가 주어졌으니 다양한 알파와 베타에 대한 오류를 계산할 수 있다.

def error(alpha, beta, x_i, y_i):
    """실제 결과가 y_i라고 할 때,
    beta*x_i+alpha로 계산된 예측값의 오류"""
    return y_i - predict(alpha, beta, x_i)

우리가 알고 싶은 것은 데이터 전체에서 발생하는 오류값이지만 모든 오류값을 더할 경우 문제가 생긴다. 만약 x_1의 예측값이 너무 높고 x_2의 예측값이 너무 낮으면 오류값이 서로 상쇄되기 때문이다. 그래서 오류값의 제곱을 더해줘야 한다.

def sumOfSquareErrors(alpha, beta, x, y):
  return sum(error(alpha, beta, x_i, y_i) ** 2
             for x_i, y_i in zip(x,y)

최소자승법은 sumOfSquaredErrors를 최소화 해주는 알파와 베타 값을 찾는 것을 뜻한다. 미분이나 대수학을 사용하면 오류를 최소화하는 알파와 베타를 찾을 수 있다.

from stats import correlation, standard_deviation, mean, de_mean

def predict(alpha, beta, x_i):
    return beta * x_i + alpha

def error(alpha, beta, x_i, y_i):
    """실제 결과가 y_i라고 할 때, beta*x_i+alpha로 계산된 예측값의 오류"""
    return y_i - predict(alpha, beta, x_i)\

def sumOfSquaredErrors(alpha, beta, x, y):
    return sum(error(alpha, beta, x_i, y_i) ** 2
               for x_i, y_i in zip(x,y))

def leastSquaresFit(x, y):
    """x와 y가 학습 데이터로 주어졌을 때
    오류의 제곱 값을 최소화해 주는 알파와 베타 계산"""
    beta = correlation(x, y) * standard_diviation(y) / standard_deviation(x)
    alpha = mean(y) - beta * mean(x)
    return alpha, beta

\[\sigma = \sqrt{\operatorname{E}(X-\operatorname{E}(X))^2} = \sqrt{\operatorname{E}(X^2) - (\operatorname{E}(X))^2}\]

(표준편차 다시 짚기)
산포도를 나타내는 수치로 분산의 제곱근.
확률 변수 X의 표준편차는 다음과 같다.

오류 최소화 방법이 왜 말이 될까? 독립 변수 x의 평균이 주어지면, 알파는 종속 변수 y의 평균을 예측해 준다. 베타는 입력 변수가 standard_deviation(x)만큼 증가한다면 예측값 또한 correlation(x,y) x standard_deviation(y)만큼 증가한다는 것을 의미한다. x와 y가 완벽한 양의 상관관계를 지닌다면, x가 1 표준편차 증가할 때마다 y또한 1 표준편차만큼 증가한다. x와 y가 완벽한 음의 상관관계를 지닌다면, x가 증가할 때 y가 감소한다. 상관 관계가 0이라면 베타는 0이 되며, x가 예측에 아무 영향이 없다는 걸 의미한다.

이제 데이터를 준비해서 이 방법을 적용해보자.

num_friend = [some data set]
daily_minutes = [some data set]
alpha, beta = leastSquaredFit(num_friends, daily_minutes)
>> alpha : 22.94755241346903
>> beta : 0.903865945605865

alphax = []

for i in range(51):
    alphax.append((i+alpha)*beta)

from matplotlib import pyplot as plt
plt.scatter(num_friends, daily_minutes)
plt.plot(alphax)
plt.title("Simple linear regression model")
plt.xlabel("# of friends")
plt.ylabel("minutes per day")
plt.axis([0,50,0,105])
plt.show()

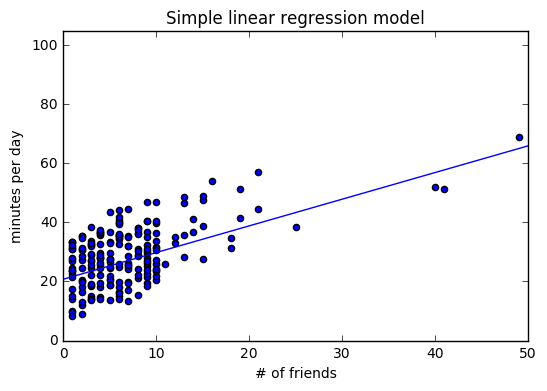
Simple linear regression model

이제 모델이 적합한지 확인하기 위해 그래프를 살펴보는 것 이외의 일을 해보자. 보통은 결졍계수(R 제곱 값)라는 수치를 사용한다. 결정계수는 종속 변수의 총 변화량 중 모델이 잡아낼 수 있는 변화량의 비율을 의미한다.

def totalSumOfSquares(y):
    """평균을 기준으로 y_i의 변화량을 제곱한 값의 총합"""
    return sum(v ** 2 for v in de_mean(y))

def rSquared(alpha, beta, x, y):
    """모델이 잡아낼 수 있는 변화량의 비는 1 - 모델이 잡아낼 수 없는 변화량의 비이다."""
    """모델이 잡아낼 수 없는 변화량 = 오류 / 평균 기준 y_i 변화량의 총값"""
    return 1.0 - (sumOfSquaredErrors(alpha, beta, x, y) / totalSumOfSquares(y))

    rSquared(alpha, beta, num_friends, daily_minutes)
    >>0.3291078377836305

계산된 R 제곱 값이 0.329… 양수이므로 모델은 데이터에 어느정도 적합하지만 더 중요한 요소가 있다는 걸 의미한다.

경사하강법 이용하기

theta = [alpha, beta]로 설정하면 경사 하강법을 통해 모델을 만들 수 있다.

from gradient_descent import minimize_stochastic
import random

def squaredError(x_i, y_i, theta):
    alpha, beta = theta
    return error(alpha, beta, x_i, y_i) ** 2

def squaredErrorGradient(x_i, y_i, theta):
    alpha, beta = theta
    return [-2 * error(alpha, beta, x_i, y_i),       # 알파에 대한 편미분
            -2 * error(alpha, beta, x_i, y_i) * x_i]  # 베타에 대한 편미분

random.seed(0)
theta = [random.random(), random.random()]
alpha, beta = minimize_stochastic(squaredError,
                                 squaredErrorGradient,
                                 num_friends,
                                 daily_minutes,
                                 theta,
                                 0.0001)

print(alpha)
>>22.93746417548679
print(beta)
0.9043371597664965

물론 위의 경사하강법에서는 $\theta$ 값을 무작위로 선정했기 때문에 모델의 성능이 상승되진 않았다.

최대우도추정법

최소자승법을 사용한 이유가 뭘까? 최대우도추정법(maximum likelihood estimation, MLE) 때문이다.
임의의 파라미터 $\theta$에 의존하는 분포에서 $v_1,...,v_n$이란 표준 데이터가 주어졌다고 하자.

\[p(v_1,...,v_n|\theta)\]

$\theta$를 모르고 표본이 주어졌을 때 $\theta$가 발생할 likelihood로 바꿔서 생각해볼 수 있다.

\[L(\theta)|v_1,...,v_n)\]

이 경우 적절한 $\theta$는 likelihood를 최대화하는 값이다. 즉 관측된 데이터가 발생할 경우를 가장 높게 만들어 주는 값이란 뜻이다. 확률질량함수(PMF) 대신 확률밀도함수(PDF)를 사용하는 연속형 분포에도 이를 적용할 수 있다. 회귀 분석으로 다시 가보자. 대부분의 회귀 분석에는 오류를 평균이 0이고 표준편차가 $\sigma$인 정규분포를 따른다고 가정한다. 이 때 (x_i, y_i)가 관측될 likelihood는 다음과 같다.

\[f(\alpha, \beta |x_i,y_i,\sigma)= \frac{1}{\sqrt{2\pi} \sigma} exp(-(y_i-\alpha - \beta x_i)^2/2\sigma^2)\]

전체 데이터에 대한 likelihood를 모두 곱한 값이다. 그리고 오류의 제곱 값을 최소화하는 알파와 베타가 계산되는 지점이 likelihood가 최대화되는 지점이다. 이런 가정을 따르면 오류의 제곱 값을 최소화하는 것은 관측된 데이터가 발생할 likelihood를 최대화하는 것과 같다.