- 본문의 내용은 Data Science from scratch(밑바닥부터 시작하는 데이터 과학)을 읽고 작성했습니다.
- 본문의 소스코드의 일부는 Joel Grus의 Github에서 Unlicensed 라이선스로 배포되고 있습니다.
당신은 내가 다음 노트북으로 어느 모델을 구매할 지 예측해 볼 수 있는가? 당신이 나에 대해 아무것도 모른다고 해도, 내 주변 개발자들이 무슨 노트북을 쓰고 있는지를 알고 있다면 내가 무엇을 구매할지도 어느 정도 짐작해 볼 수 있다. 맥OS를 좋아하는 개발자들을 주변에 두고 있기 때문에, 나 역시 새로운 맥북을 구매할 것이라고 한다면 그것은 그럴듯한 주장이다.
그럼 나에 대해 아는 것이 주변 개발자들의 노트북 뿐만이 아니라, 나이, 소득, 여태까지 가진 노트북의 수라고 가정해보자. 나의 지름은 이런 특성들에 어느 정도 영향을 받거나 결정되므로 이 모든 특성을 고려해 가장 가까운 개발자들(이웃)만 선별한다면 모든 개발자(이웃)들을 고려했을 때보다 더 나은 추정을 할 수 있다. 이것이 k-NN의 숨겨진 논리이다.
모델
k-NN(k-Nearest Neighbors, k-근접이웃)은 단순한 예측 모델의 하나이다. 수학적 가정과 엄청난 컴퓨터가 필요하지 않다. 다만,
- 거리를 재는 방법
- 서로 가까운 점들이 유사하다는 가정
이 필요하다. 많은 모델들은 데이터의 패턴을 찾기 위해 전체 데이터 셋을 참조해야 하지만 k-NN은 궁금한 점 주변의 데이터만 보면 되기에 많은 데이터를 뒤지지 않아도 괜찮다.
하지만 k-NN은 어떤 상황의 원인을 밝히는 데는 도움이 되지 않는다. 어떤 모델은 나의 나이-소득-여태까지 가진 노트북의 수가 새 노트북 구매 결정에 영향을 끼친다고 얘기해 주지만, k-NN은 그렇지 않다.
보통 데이터 포인트와 그에 대한 레이블(label) 정보가 주어진다. 레이블은 어떤 조건(비싼가? 예쁜가?)을 만족했는지에 따라 참, 거짓이 되거나 카테고리가 될 수 있다. 노트북의 모델명이거나 가장 좋아하는 프로그래밍 언어일 수도 있다.
이번 실험의 경우 데이터 포인트는 벡터이다. 따라서 유클리드 거리 함수를 사용할 수 있다.
k-NN에서는 다음과 같은 선형대수 함수, 평균 함수를 참조할 것이다.
#linear_algebra.py
def vector_subtract(v, w):
"""subtracts two vectors componentwise"""
return [v_i - w_i for v_i, w_i in zip(v,w)]
def dot(v, w):
"""v_1 * w_1 + ... + v_n * w_n"""
return sum(v_i * w_i for v_i, w_i in zip(v, w))
def sum_of_squares(v):
"""v_1 * v_1 + ... + v_n * v_n"""
return dot(v, v)
def squared_distance(v, w):
return sum_of_squares(vector_subtract(v, w))
def distance(v, w):
return math.sqrt(squared_distance(v, w))
#stats.py
def mean(x):
return sum(x) / len(x)
그럼 직접 코드를 작성해보자.
from collections import Counter
from linear_algebra import distance
from stats import mean
import math, random
import matplotlib.pyplot as plt
# find most frequent one >> nearest K
# 가장 빈도 수가 높은(가까운) k를 찾는다.
def raw_majority_vote(labels):
votes = Counter(labels)
winner, _ = votes.most_common(1)[0]
return winner
raw_majority_vote([1,1,1,1,1,2,2,2,2,2])
>>1
# 값이 같은 항목들을 제대로 처리하지 못한다.
# 이럴 땐 다음과 같은 선택을 할 수 있다.
# - 여러 1등 중 임의로 하나를 정한다.
# - 거리를 가중치로 사용해서 거리 기반 투표를 한다.
# - 단독 1등이 생길 때까지 k를 하나씩 줄인다. >> 구현
def majorityVote(labels):
voteCounts = Counter(labels)
winner, winnerCount = voteCounts.most_common(1)[0]
num_winners = len([count for count in voteCounts.values()
if count is winnerCount])
if num_winners is 1:
return winner
else:
return majorityVote(labels[:-1])
majorityVote([5,5,5,5,1,1,1,1,2,2,2,2,3,3,3,3,4,4,4,4])
>>5
동기부여 : 가장 인기 있는 프로그래밍 언어
각 대도시 사람들이 선호하는 프로그래밍 언어의 데이터가 있다고 쳐보자.
# 데이터는 [경도, 위도], 선호하는 프로그래밍 언어 꼴로 이루어져있다.
cities = [(-위도,경도,'python')...] # 계속 이어짐
cities = [([longitude, latitude], language) for longitude, latitude, language in cities]
def knnClassify(k, labeledPoints, newPoint):
"""labeldPoints는 데이터 포인트, 레이블 쌍으로 구성됨."""
"""labeldPoints를 가까운 순서부터 먼 순서로 정렬"""
byDistance = sorted(labeledPoints,
key=lambda pointLabel: distance(pointLabel[0], newPoint))
kNearest = [label for _, label in byDistance[:k]]
return majorityVote(kNearest)
def testkNN(klist):
for k in klist:
numCorrect = 0
for location, actualLanguage in cities:
otherCities = [otherCity
for otherCity in cities
if otherCity != (location, actualLanguage)]
predictedLanguage = knnClassify(k, otherCities, location)
if predictedLanguage == actualLanguage:
numCorrect += 1
print(k, "neighbors[s]:", numCorrect, "correct out of", len(cities))
testkNN([1,3,5,7])
>>1 neighbors[s]: 40 correct out of 75
>>3 neighbors[s]: 44 correct out of 75
>>5 neighbors[s]: 41 correct out of 75
>>7 neighbors[s]: 35 correct out of 75
# k 값을 3으로 정했을 때의 정확도가 가장 높다.
# 3의 주변 수에 대해서 다음과 같은 시도도 해볼 수 있다.
testkNN([2,4])
print(44/75)
>>2 neighbors[s]: 40 correct out of 75
>>4 neighbors[s]: 44 correct out of 75 # k=4일 때의 결과값이 k=3일 때와 같다.
>>0.5866666666666667 # 약 59%.
차원의 저주
k-NN은 차원의 저주(curse of dimensionality) 때문에 고차원에서 문제를 맞이한다. 데이터가 고차원이라는 것은 다루는 공간이 엄청나게 크다는 것이고, 그 때문에 데이터들이 서로 ‘근접(near)’하지 않게 된다. 이 현상을 관찰하기 위해 다양한 차원으로 임의의 점 2개를 생성해 거리를 재어보자.
# 무작위 지점(차원)
def randomPoint(dim):
return [random.random() for _ in range(dim)]
# 무작위 지점과 지점간의 거리(차원, 쌍)
def randomDistances(dim, numPairs):
return [distance(randomPoint(dim), randomPoint(dim)) for _ in range(numPairs)]
dimensions = range(1, 101)
avgDistances = []
minDistances = []
random.seed(0)
for dim in dimensions:
distances = randomDistances(dim, 10000)
avgDistances.append(mean(distances))
minDistances.append(min(distances))
plt.plot(avgDistances, color='green', linestyle='solid', label='avg distance')
plt.plot(minDistances, color='blue', linestyle='solid', label='min distance')
plt.title("10,000 Random distances")
plt.xlabel("# of dimensions")
plt.legend(loc=9)
plt.show()
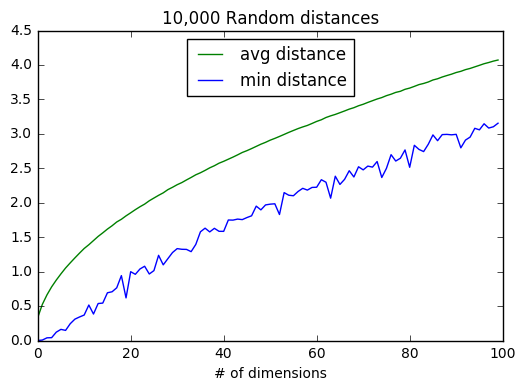
차원이 증가할수록 점들 간 평균 거리도 증가하지만 더 큰 문제는 최근접거리와 평균 거리의 비율이다.
min_avg_ratio = [min_dist, avg_dist
for min_dist, avg_dist in zip(minDistances, avgDistances)]
plt.plot(min_avg_ratio, color='blue', linestyle='solid')
plt.title("Minimum Distance / Average Distance")
plt.xlabel("# of dimensions")
plt.show()
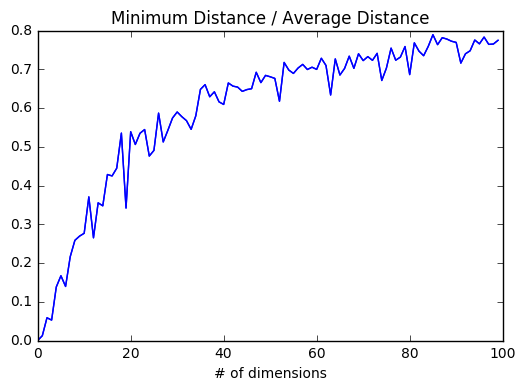
저차원에서는 근접이웃들이 평균 거리에 비해 월등히 가깝다. 하지만 두 점이 ‘가깝다’고 말하려면 모든 차원에 대해 가까워야 하기 때문에 차원이 추가되는 것은 (그것이 노이즈라 해도) 두 점이 가까울 수 있는 가능성을 현저히 줄어드는 것을 의미한다. 고차원일 때는 근접이웃들이 평균 거리와 큰 차이가 나지 않게 되고, 그렇게 되면 가깝다는 것이 별 의미를 갖지 않게 된다.
고차원 문제를 바라볼 수 있는 다른 관점에는 공간의 성김(sparsity)이 있다.
1차원 공간을 생각해보자. 0과 1까지의 구간이 하나의 선이라고 볼 때, 0과 1사이의 임의의 구간 50개에 점을 찍으면 구간이 어느정도 채워지는 느낌이 들 것이다. 하지만 2차원 평면에 50개의 점으로 산점도를 찍는다고 하면 그다지 채워진 느낌이 들지 않을 것이다. 이는 3차원 공간에서 더 심화되고, 그 다음 고차원 공간에서도 마찬가지이다.
그렇기 때문에 k-NN모델을 고차원 데이터와 함께 사용할 때에는 고차원 데이터를 축소하는 과정이 필요하다.