- 본문의 내용은 Data Science from scratch(밑바닥부터 시작하는 데이터 과학)을 읽고 작성했습니다.
- 본문의 소스코드의 일부는 Joel Grus의 Github에서 Unlicensed 라이선스로 배포되고 있습니다.
확률
일정한 조건 아래에서 어떤 사건이나 사상이 일어날 가능성의 정도. 또는 그런 수치. 수학적으로는 1을 넘을 수 없고 음이 될 수도 없다. 확률 1은 항상 일어남을 의미하고, 확률 0은 절대로 일어나지 않음을 의미한다.
- 표준국어대사전
종속성과 독립성
동전을 던졌을 때 첫 동전에서 앞면이 나왔다고 두 번째 동전에서 앞면이 나올지 아닐지는 알 수 없다. 이 경우를 독립적이라고 한다. 하지만 첫 동전에서 앞면이 나왔을 때 두 동전 모두 뒷면이 나올 확률은 0이다. 이를 종속적이라고 한다. (가능성P, 사건 E,F)
독립 사건이 동시에 일어날 확률
\[P(E,F) = P(E)P(F)\]또 두 사건이 반드시 독립 사건이 아닐 수도 있고 사건 F의 확률이 0이 아닌 경우 사건 E가 발생할 조건부 확률은 아래와 같다.(P(E|F)는 F가 일어난 것을 전재로 E가 일어날 확률)
조건부 확률
\[P(E|F) = P(E,F)/P(F)\]동전을 두 번 던질 때, 첫 번째 동전이 앞면일 경우(F), 모든 동전이 앞면일 확률(D)은 다음과 같다.
\[P(D|F) = P(D,F)/P(F) = P(D)/P(F) = 1/2\]동전이 최소 하나 이상 앞면일 경우(H), 모든 동전이 앞면일 확률(D)은 다음과 같다.
\[P(D|H) = P(D,H)/P(H) = P(D)/P(H) = 1/3\]Write in code
import random
def random_face():
return random.choice(["back","front"])
both_front = 0
first_front = 0
either_front = 0
random.seed()
for _ in range(10000):
f = random_face()
s = random_face()
if f == "front":
first_front += 1
if f == "front" and s == "front":
both_front += 1
if f == "front" or s == "front":
either_front += 1
큰 수의 법칙
‘표본의 숫자가 많을수록 실사건의 확률이 통계적 예측에서 오차가 줄어든다.’
예를 들어서 동전 던지기를 2번 했을 때 모든 동전이 앞면일 가능성은 1/2**2, 1/4이지만, 10번 했을 때의 가능성은 0.0009765625로 희박하다. 동전 던지기를 반복할 수록 실험의 결과는 동전의 통계치(1/2)에 근접해간다.
print("P(both|first_front)", both_front / first_front)
print("P(both|first_front)", both_front / either_front)
>>P(both|first_front) 0.48842229199372056(~0.5)
>>P(both|first_front) 0.3275862068965517(~0.333..)
베이즈 정리
사건 F가 발생했다는 가정하에 사건 E가 발생할 확률을 요구할 때, 사건 E가 발생했다는 가정하에 사건 F가 발생한 확률을 통해 구해낼 수 있다.
\[P(E|F) = P(E,F)/P(F) = P(F|E)P(E)/P(F)\]사건 F를 ‘사건 F와 사건 E가 모두 발생하는 경우’와 ‘사건 F는 발생하지만 사건 E는 발생하지 않는 경우’로 나눌 수 있다. 만약 사건 E가 발생치 않는 경우를 ㄱE라고 하면 다음과 같은 식이 된다.
\[P(F) = P(F,E) + P(F,ㄱE)\]이를 이용하면 베이즈 정리는 다음과 같이 정리될 수 있다.
\[P(E|F) = P(F|E)P(E) / [P(F|E)P(E) + P(F|ㄱE)P(ㄱE)]\]F이후 E가 일어날 확률 =
E이후 F가 일어날 확률 / [
E이후 F가 일어날 확률 x E가 일어날 확률
+ E가 일어나지 않았을 때 F가 일어날 확률 x E가 일어나지 않을 확률]
상상
10000명 중에 1명이 걸리는 병이 있고, 이 병에 따른 진단 양성판정(T)과 질병에 걸린 경우(D)가 있을 때 99%의 경우 정확한 판단을 내리는 검사기가 있다.
양성 판정일 경우, 실제로 병에 걸렸을 확률을 베이즈 정리로 풀어 보면 다음과 같다.
\[P(D|T) = P(T|D)P(D) / [P(T|D)P(D) + P(T|ㄱD)P(ㄱD)]\]진단 시 발병률 = 발병 시 진단률x발병률/[발병시 진단률x발병률+오진률x미발병률]
진단 시 발병률 = 0.99 x 0.0001/[0.99 x 0.0001 + 0.01 x 0.9999] x 100 = 0.98…
양성판정을 받은 사람 중 실제로 질병에 걸린 사람은 0.98%정도에 그친다.
풀어쓰기 :
100만 명의 사람이 검사를 할 경우 100명이 발병자라고 예측, 이 중 99명은 양성 판정을 받는다. 반대로 999,900명은 질병에 걸리지 않았으나 이 중 1%에 해당하는 9999명은 양성 판정을 받았을 것이다. 즉 양성 판정을 받은 99 + 9999명 중 실제로는 99명만 질병을 갖고 있다.
확률변수
확률 변수란 특정 확률분포와 연관된 변수를 뜻한다. 간단하게 동전의 앞면이 나오면 1이고 동전의 뒷면이 나오면 0인 확률변수를 들 수 있다. 조금 더 복잡한 경우라면 동전을 10번 던져서 나온 앞면의 수 등을 생각할 수 있다.
확률 변수와 이어진 확률분포는 각 변수의 값에 해당되는 값을 계산해 준다. 동전 던지기를 예로 들어 값이 0인 확률변수의 확률은 0.5이며 값이 1인 확률변수의 확률 또한 0.5이다. range(10)의 경우 0부터 9까지 변수 값에 대한 확률은 0.1이다. (10%)
모든 확률변수의 확률을 특정 확률변수의 값으로 가중평균한 값인 확률변수는 기댓값이라고 한다.
예컨데 동전 던지기에서 확률변수의 기댓값은 1/2(= 0x1/2 + 1x1/2)이다. 그리고 range(10)에서의 기댓값은 ( 0x1/10 + 1x1/10 + 2x1/10 … + 9x1/10) 4.5이다.
확률변수 또한 사건처럼 조건부 확률을 구할 수 있다. 두 동전의 앞/뒷면으로 예시를 들어보자.
만약 X라는 확률변수가 앞면의 수를 나타낸다면 X가 0일 확률은 1/4, 1일 확률은 1/2, 그리고 2일 확률은 1/4이다.
새로운 확률변수 Y가 최소 하나의 동전이 앞면일 때 전체 앞면인 동전의 수를 나타낸다면, Y가 1일 확률은 2/3, 2일 확률은 1/3이다.
Z가 첫 동전이 앞면일 때 전체 앞면의 수를 나타내면 Z가 1일 확률은 1/2, 2일 확률도 1/2이다.
연속 분포
동전 던지기는 각각의 결과에 확률이 계산되는 이산형 분포(discrete distribution)을 따른다. 하지만 대게의 경우 연속적인 결과에 대한 분포를 통해 모델을 만들 것이다. 균등 분포(Uniform destribution)은 0과 1사이의 모든 값에 동등한 비중을 준 분포이다.
0과 1 사이에는 무한히 많은 숫자가 존재해 숫자 하나의 비중은 ~0일 것이다. 그렇기 때문에 밀도함수를 특정 구간에서 적분한 값으로 확률을 나타내는 확률밀도함수(probability density function, pdf)로 연속 분포를 표현해보자.
#다음은 균등 분포의 학률밀도함수이다.
def uniform_pdf(x):
return 1 if x >= 0 and x < 1 else 0
"""
확률변수의 값이 특정 값보다 작거나 클 확률을 나타내는 함수는
누적분포함수(Cumulative distribution function, cdf)라고 한다.
"""
def uniform_cdf(x):
if x < 0: return 0 # 균등분포의 확률은 0을 초과해야 함
elif x < 1: return x # 예시 P(X <= 0.4) = 0.4
else: return 1 # 균등분포의 확률 < 1
정규분포
정규분포(normal destribution)는 곡선 모양의 분포로, 평균인 μ, 표준편차 σ로 정의된다.
평균은 종의 중심이 어딘지를 나타내며, 표준편차는 종의 폭이 얼마나 넓은지를 나타낸다. (exp = e**x)
다음과 같이 구현할 수 있다.
from matplotlib import pyplot as plt
from math import sqrt, pi, exp, erf
def normal_pdf(x, mu=0, sigma=1):
sqrt_two_pi = sqrt(2*pi)
return (exp(-(x-mu) ** 2 / 2 / sigma ** 2) / (sqrt_two_pi * sigma))
xs = [x / 10.0 for x in range(-50, 50)]
plt.plot(xs, [normal_pdf(x,sigma=1) for x in xs],'-',label='mu=0,sigma=1 - standard')
plt.plot(xs, [normal_pdf(x,sigma=2) for x in xs],'--',label='mu=0,sigma=2')
plt.plot(xs, [normal_pdf(x,sigma=0.5) for x in xs],':',label='mu=0,sigma=0.5')
plt.plot(xs, [normal_pdf(x,mu=-1) for x in xs],'-.',label='mu=0,sigma=1')
plt.legend(prop={'size': 8})
plt.title("Various Normal PDFs")
plt.show()
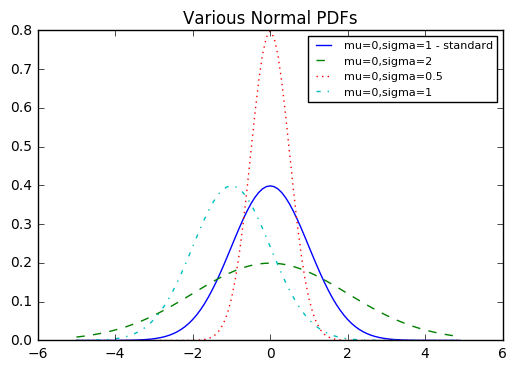 그래프에서 파란색 실선의 정규분포를 표준정규분포라고 한다.(mu=0, sigma=1)
그래프에서 파란색 실선의 정규분포를 표준정규분포라고 한다.(mu=0, sigma=1)
만약 Z가 표준정규분포의 확률변수를 나타낸다면 다음처럼,
X도 평균이 mu이고 표준편차가 sigma인 정규분포로 표현할 수 있다. 반대로 X가 평균이 mu이고 표준편차가 sigma인 정규분포의 확률변수를 나타낸다면, 다음과 같이 선형변환을 통해 표준정규분포로 표현할 수 있다.
\[Z = (X - \mu)/\sigma\]정규분포의 누적분포함수를 구현하기 위해서 파이썬의 math.erf(오차함수)를 사용할 수 있다.
def normal_cdf(x, mu=0, sigma=1):
return (1 + erf((x - mu) / sqrt(2) / sigma)) / 2
xs = [x / 10.0 for x in range(-50, 50)]
plt.plot(xs,[normal_cdf(x,sigma=1) for x in xs],'-',label='mu=0, sigma=1')
plt.plot(xs,[normal_cdf(x,sigma=2) for x in xs],'--',label='mu=0, sigma=2')
plt.plot(xs,[normal_cdf(x,sigma=0.5) for x in xs],':',label='mu=0, sigma=0.5')
plt.plot(xs,[normal_cdf(x,mu=-1) for x in xs],'-.',label='mu=-1, sigma=1')
plt.legend(loc=2,prop={'size':8}) # location 1 2 3 4 택1
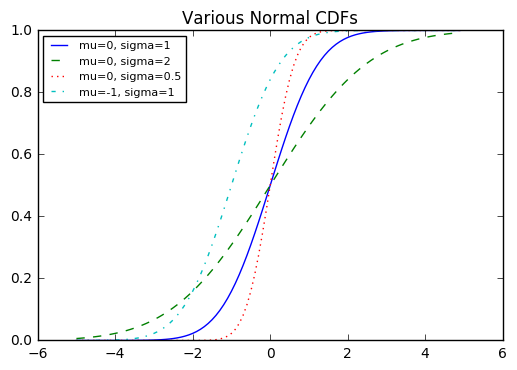
plt.title("Various Normal CDFs")
plt.show()
def inverse_normal_cdf(p, mu=0, sigma=1, tolerance=0.00001):
"""이진 검색을 통해 역함수 근사"""
# 표준정규분포가 아니라면 표준정규분포로 변환
if mu != 0 or sigma != 1:
return mu + sigma * inverse_normal_cdf(p, tolerance=tolerance)
low_z, low_p = -10.0, 0 # normal_cdf(-10)는 0에 근접
hi_z, hi_p = 10.0, 1 # normal_cdf(10)는 1에 근접
while hi_z - low_z > tolerance:
mid_z = (low_z + hi_z) / 2
mid_p = normal_cdf(mid_z)
if mid_p < p:
# 중간 값이 작으면 더 큰 값 검색
low_z, low_p = mid_z, mid_p
elif mid_p > p:
hi_z, hi_p = mid_z, mid_p
else:
break
return mid_z
중심극한정리
동일한 분포에 대한 독립적인 확률변수의 평균을 나타내는 확률변수가 대략적으로 정규분포를 따른다.
중심극한정리를 보다 이해하기 쉽도록 이항 확률변수(binomial random variable)를 예로 들자. 이항 확률변수는 n과 p 두 가지 파라미터로 구성되어 있다. 이항 확률변수는 단순히 n개의 독립적인 베르누이 확률변수를 더한 것이다.
각 베르누이 확률변수의 값은 p의 확률로 1, 1 - p의 확률로 0이 된다.
def bernoulli_trial(p):
return 1 if random.random() < p else 0
def binomial(n, p):
return sum(bernoulli_trial(p) for _ in range(n))
# n이 적당히 클 때 mu는 np
binomial(10000, 0.5)
>>4996(~5000)
베르누이 확률변수의 평균은 p이며, 표준편차는 \(\sqrt {p(1 - p)}\)이다. 중심극한정리는 n이 적당히 크다면 이항 확률변수는 대략 평균이 \(\mu=np\)이고 표준편차가 \(\sigma = \sqrt{np(1 - p)}\)인 정규분포의 확률변수와 비슷해진다는 것을 알려준다.
from collections import Counter
def make_hist(p, n, num_points):
data = [binomial(n, p) for _ in range(num_points)]
histogram = Counter(data)
plt.bar([x - 0.4 for x in histogram.keys()],
[v / num_points for v in histogram.values()],
0.8,
color='0.75')
mu = p * n
sigma = sqrt(n * p * (1 - p))
# 근사된 정규분포를 라인 차트로 표현
xs = range(min(data), max(data) + 1)
ys = [normal_cdf(i + 0.5, mu, sigma) - normal_cdf(i - 0.5, mu, sigma)
for i in xs]
plt.plot(xs,ys)
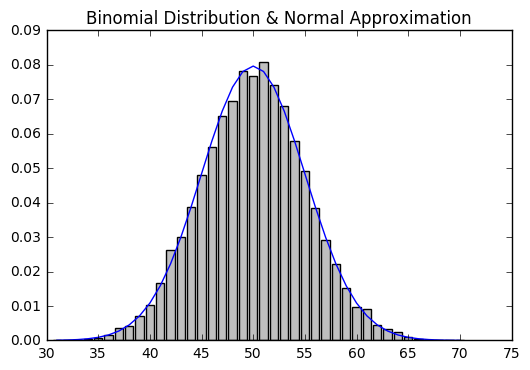
plt.title("Binomial Distribution & Normal Approximation")
plt.show()
make_hist(0.5, 100, 10000)