- 본문의 내용은 Data Science from scratch(밑바닥부터 시작하는 데이터 과학)을 읽고 작성했습니다.
- 본문의 소스코드의 일부는 Joel Grus의 Github에서 Unlicensed 라이선스로 배포되고 있습니다.
통계학
자료의 학문(Study of data)
관찰과 실험으로부터 얻어진 자료에서 질 좋은 정보를 적출하기 위한 것이다. 이를 위해 통계에서는 야생의 데이터(Raw data)를 어떻게 얻어내는지(Crawling), 그 데이터를 어떻게 길들이는지, 전체에서 뽑아낸 몇 개의 자료만으로 전체에 대한 정보를 완전히 알아내는 것을 배우는 학문이다.
(위 설명만으로도 데이터마이닝에 왜 통계학이 중요한지는 입증되는 것 같다.)
귀납논증의 학문
통계는 귀납논증의 학문이다. 항상 반례 가능성을 가지고 있다. 설령 통계적으로는 100%라도 그것이 전수조사가 아니면 반례가 존재할 가능성을 완전히 배제할 수는 없다. 반면 너무 자명하게 100% 혹은 0%인 경우도 통계적인 의미가 없다. 조사의 필요성이 없기 때문. “100세 이상 인간의 사망률은 100%다” 같은 명제가 여기 해당한다. 또한 일반적으로 봤을 때 가장 무의미한 수치는 50%이다. 특정한 결론을 내릴 수가 없기 때문. 아이러니하게도 확실한 것을 중요시하는 수학과는 다른 점이 있다.
왜곡
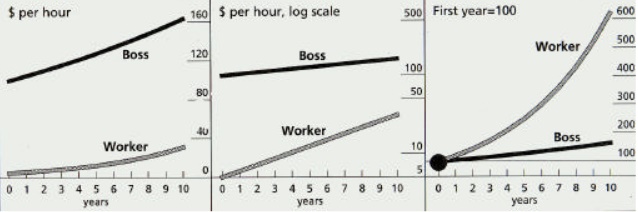
올바르고 직관적인 통계, 시각화가 필요하다.
시각화로 모자랄(불완전) 때
from matplotlib import pyplot as plt, pylab
from numpy import random
from collections import Counter
num_friend = []
for i in range(100):
num_friend.append(random.randint(1,50))
friend_counts = Counter(num_friend)
xs = range(51)
ys = [friend_counts[x] for x in xs]
plt.bar(xs, ys, color='pink')
plt.axis([0, 51, 0, 10])
plt.title("Historgram of friend counts")
pylab.xlabel("Number of friends")
pylab.ylabel("Number of People")
plt.show()
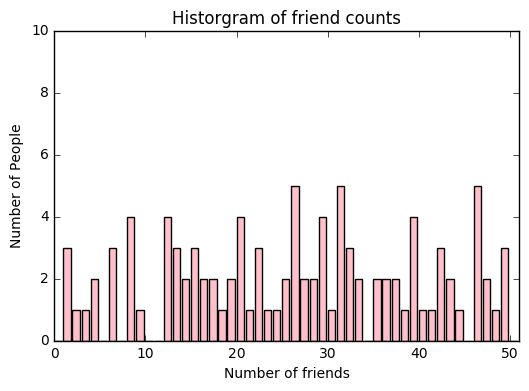
히스토그램의 막대가 데이터에 대한 설명으로 와닿지 않을 땐 어떻게 해야 할까? 히스토그램에 대한 통계치 를 계산해보자.
num_points = len(num_friend)
num_points # 데이터의 갯수
>>100
largest_value = max(num_friend)
smallest_value = min(num_friend)
print(largest_value)
print(smallest_value)
>>49
>>1
# 정렬된 list를 사용하면 어떨까?
sorted_values = sorted(num_friend)
smalles_value = sorted_values[0]
second_smallest_value = sorted_values[1]
largest_value = sorted_values[-1]
second_largest_value = sorted_values[-2]
중심 경향성
데이터의 중심이 어디 있는지를 나타내는 중심 경향성(central tendency)지표를 파악해야 한다. 대부분의 경우, 데이터의 값을 데이터의 수로 나눈 평균을 사용하게 된다.
def mean(x):
return sum(x) / len(x)
mean(num_friend)
>>25.9
가끔은 중앙값(median)도 필요하다.
데이터의 수가 홀수일 경우 정 가운데의 데이터, 데이터가 짝수일 경우 가운데의 두 데이터의 평균이 중앙값이 된다.
data1 = [1,2,3,4,5]
medianodd = data1[len(data1)//2]
data2 = [1,2,3,4,5,6]
medianeven = (data2[len(data2)//2-1]+data2[len(data2)//2])/2
print(medianodd)
print(medianeven)
>>3
>>3.5
median3=(num_friend[len(num_friend)//2]+num_friend[len(num_friend)//2-1])/2
median3
>30.0
# 이 median은 잘못됐다. 데이터를 정렬하지 않았으니까!
# 함수로 정의해보자.
def median(v):
"""v의 중앙값을 계산"""
n = len(v)
sorted_v = sorted(v)
midpoint = n // 2
if n % 2 is 1:
return sorted_v[midpoint]
else:
return (sorted_v[midpoint-1]+sorted_v[midpoint])/2
# 중앙값
print(median(num_friend))
>>26.0
# 평균값
print(mean(num_friend))
>>25.9
중앙값을 사용할 때도 있겠지만, 평균은 중앙값보다 계산하기도 간편하거니와 데이터가 변경되었을 때의 값 변화가 자연스럽다. 새로운 데이터 값이 주어졌을 때 값이 e(평균 이하치)라면 평균은 e/n만큼 증가할 것이다. 반면 중앙값을 갱신하기 위해선 데이터를 다시 정렬해야 한다.(Quicksearch 알고리즘을 사용하면 정렬없이 중앙값을 찾을 수 있다.) 주어질 값이 어떨지 모르며, 주어진 데이터에 중앙값이 변하지 않을 수도 있다.
하지만 평균은 이상치에 민감하다. num_friend 네트워크에 200명의 친구를 가진 새 사용자가 있다고 하면 평균값은 그에 맞게 증가할테지만 중앙값은 변하지 않을 것이다.
‘이상치’가 나쁜 데이터에서 평균은 데이터에 대한 잘못된 정보가 될 수 있다.
예를 들자면 1980년대 노스캐롤라이나 대학의 전공 중 지리학과가 졸업생 초봉이 가장 높은 과로 조사되었으나, 그 이유는 지리학을 전공한 ‘마이클 조던의 초봉’(이상치) 때문이었다.
또 ‘분위‘는 중앙값을 포괄하는 개념으로, 데이터의 특정 백분위보다 낮은 값을 뜻한다. (중앙값은 상위 50%의 데이터보다 작은 값)
def quantile(v, p):
"""v의 p에 속하는 값 반환"""
p_index = int(p * len(v))
return sorted(v)[p_index]
quantile(num_friend, 0.01)
>>1
# 또 최빈값(Mode, most frequent value)을 살펴볼 수도 있다.
def mode(v):
counts = Counter(v)
max_count = max(counts.values())
return [v_i for v_i, count in counts.items()
if count == max_count ]
mode(num_friend)
>> [26, 31, 46]
# 하지만 '평균'이 가장 자주 사용된다.
산포도(mountain berry? 맛있겠다!)
산포도(dispersion)은 데이터가 얼마나 퍼져 있는지를 나타낸다. 0과 근접한 값일 수록 데이터는 퍼져 있지 않다는 의미이며 큰 값이면 매우 퍼져 있다고 해석할 수 있는 통계치이다.
가장 큰 값과 가장 작은 값의 차이를 나타내는 범위는 산포도를 나타내는 가장 간단한 통계치이다.
def data_range(v):
return max(v) - min(v)
data_range(num_friend)
>>48
max is min일 경우 범위 값은 0이 되며 데이터의 값이 모두 동일하며 데이터는 퍼져 있지 않음을 의미한다. 범위의 값이 크다면 max가 min에 비해 훨씬 크며 데이터가 퍼져 있음을 의미한다. 범위 또한 중앙값처럼 데이터 전체에 의존하지 않는다. 모두 0과 100으로 이루어진 데이터와 0, 100 그리고 수 많은 50으로 이루어진 데이터나 동일한 범위를 갖게 된다. 하지만 첫 번째 데이터가 분명 더 퍼져 있다. 분산(variance)은 산포도를 측정하는 약간 더 복잡한 개념으로 다음과 같이 계산된다.
\(a\mu =\operatorname{E} (X)\)가 확률변수 X의 기댓값(혹은 평균)일 때, 분산 \(\operatorname{var}(X)\) 는 다음과 같이 계산한다.
\[\operatorname{var}(X) = \operatorname{E}((X - \mu)^2)\]def dot(v, w):
return sum(v_i * w_i for v_i, w_i in zip(v, w))
def sum_of_dot(v):
dot(v, v)
def de_mean(v):
"""v의 모든 데이터 값에서 평균을 뺀다.(평균을 0으로 만들기 위해)"""
v_bar = mean(v)
return [v_i - v_bar for v_i in v]
def variance(v):
"""v는 반드시 2개 이상의 값이 있어야 한다."""
n = len(v)
deviations = de_mean(v)
return sum_of_square(deviations) / (n - 1) # n으로 계산할 경우 편향 때문에 모분산에 대한
variance(num_friend)
>>184.75757575757572
"""
한편 분산의 단위는 기존 단위의 제곱이므로
분산 대신 원래 단위와 같은 단위를 가지는
표준편차(Standard deviation)을 이용하는 경우가 많다.
"""
from math import sqrt
def standard_deviation(v):
return sqrt(variance(v))
standard_deviation(num_friend)
>>13.592555894958672
범위나 평균과 동일하게 표준편차는 이상치에 민감하게 반응한다는 문제점이 있다. 안정적인 방법으로 상위 25%값과 하위 25%값의 차를 구하는 방법 이 있다.
def interquartile_range(v):
return quantile(v, 0.75) - quantile(v, 0.25)
interquartile_range(num_friend)
>>22
상관관계
사이트 사용량 데이터를 통해 사용자가 하루에 몇 분 간 사이트를 이용했는지를 나타내는 daily_minute list를 생성했다.
이 list의 각 항목과 num-friend list의 각 항목은 같은 사용자를 의미한다.
이제 두 list의 관계를 살피자.
분산과 비슷한 개념인 공분산 을 사용해보자. 공분산은 두 변수가 각각의 평균에서 얼마나 멀리 떨어져 있는지 살펴본다.
daily_minute=[]
for i in range(100):
# 사용자는 1분에서 30분정도 사이트를 이용했다.
daily_minute.append(random.randint(1,30))
\(E(X)=\mu,E(Y)=\nu\) \(\operatorname{Cov}(X, Y) = \operatorname{E}((X - \mu) (Y - \nu)), \,\)
def covariance(x, y):
n = len(x)
"""sum(de_mean(num_friend) * de_mean(daily_minute)) / (n - 1)"""
return dot(de_mean(x), de_mean(y)) / (n - 1)
covariance(num_friend, daily_minute)
>>2.7373737373737392
공분산의 값이 양수이면 x의 값과 y의 값이 비례한다는 의미이다.
반대로 공분산의 값이 음수이면 x의 값과 y의 값은 반비례한다는 의미이다.
공분산이 0이면 그와 같은 관계가 존재하지 않는다는 것을 의미한다.
공분산의 단위는 입력 변수의 단위들을 곱해서 계산되기 때문에 이해하기 쉽지 않다. (예를 들어 친구 수X사용량에 무슨 의미가 있을까?)
만약 모든 사용자의 친구 수가 2배가 된다면 공분산의 값도 2배가 될 것이다. 하지만 두 변수의 상관관계는 변하지 않는다.(비례) 그래서 값이 얼마나 커야 공분산이 크다고 판단하는 것이 어렵다.
이러한 이유로 공분산에서 각각의 표준편차를 나눠 준 상관관계를 더 자주 살펴본다.
def correlation(x, y):
stdev_x = standard_deviation(x)
stdev_y = standard_deviation(y)
if stdev_x > 0 and stdev_y > 0:
return covariance(x, y) / stdev_x / stdev_y
else:
return 0
correlation(num_friend, daily_minute)
>>0.022435242595237437
상관관계는 단위가 없으며 항상 -1에서 1사이의 값을 지닌다. -1은 완벽한 음의 상관관계, 1은 완벽한 양의 상관관계를 의미한다.
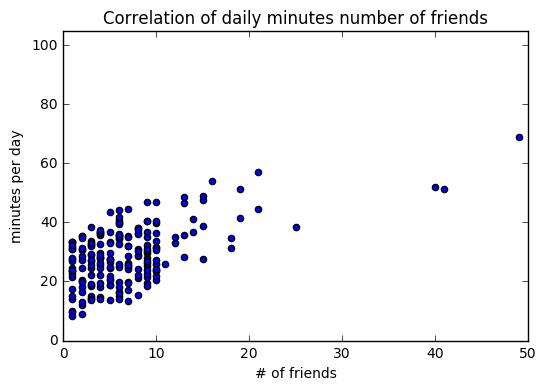
plt.scatter(num_friend, daily_minute)
plt.title("Correlation of daily minutes number of friends")
plt.xlabel("# of friends")
plt.ylabel("minutes per day")
plt.axis([0,55,0,35])
plt.show()
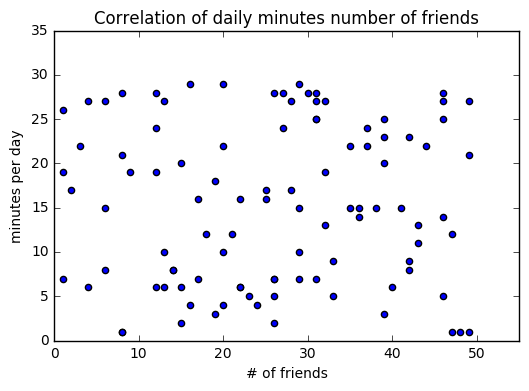
(하지만 이 경우 각 축의 값들이 무작위 정수이기 때문에 유효한 상관관계를 찾기는 힘들다. 따라서 데이터는 수집단계에서 유효한 데이터를 준비해야 한다.)
만약 상관관계가 양수이기 때문에 두 척도가 비례한다는 시각에서 그래프를 바라봤을 때, 100명의 친구가 있음에도 사이트 이용시간이 매우 낮은(ex:1분) 사용자가 있다면 이는 이상치이며 상관관계에 영향을 줄 것이다.
무작위 정수가 아닌 유효한 데이터를 사용해보고 이상치를 제거해보자.
num_friends = [some_values_too_long_to_write]
daily_minutes = [some_values_too_long_to_write]
plt.scatter(num_friends, daily_minutes)
plt.title("Correlation of daily minutes number of friends")
plt.xlabel("# of friends")
plt.ylabel("minutes per day")
plt.axis([0,105,0,105])
print(correlation(num_friends,daily_minutes))
>>0.24736957366478218
plt.show()
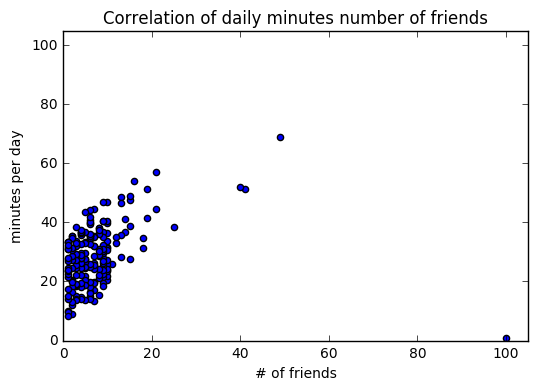
outliner = num_friends.index(100)
num_friends_good = [x for i, x in enumerate(num_friends) if i is not outliner]
daily_minutes_good = [x for i, x in enumerate(daily_minutes) if i is not outliner]
correlation(num_friends_good, daily_minutes_good)
>>0.5736792115665573
plt.scatter(num_friends_good, daily_minutes_good)
plt.title("Correlation of daily minutes number of friends")
plt.xlabel("# of friends")
plt.ylabel("minutes per day")
plt.axis([0,50,0,105])
plt.show()
# 훨씬 더 강력한 상관관계를 확인할 수 있다.
심슨의 역설
각 부분에 대한 평균이 크다고 해서 전체에 대한 평균이 클 필요는 없다.
각각의 변수(Confounding variables, 혼재 변수)에 신경을 쓰지 않으면 올바른 전체의 통계 결과를 유도할 수 없다.
(잘생긴 이목구비를 한 데 모아도 잘생긴 얼굴이 안 나올 수도 있다??)
Datascience from scratch 68p에 적절한 예시가 나와 있다.
역전의 역설이라고도 부른다.
상관관계에 대한 경고
x = [-2, -1, 0, 1, 2]
y = [2, 1, 0, 1, 2]
둘의 상관관계는 0으로 계산되지만, 분명 y는 x의 절댓값이라는 관계가 성립한다.
이런 관계는 상관관계(Correlation) 만으로는 설명할 수 없다.
또 상관관계는 연관성이 얼마나 크고 작은지 설명해주지 않는다.
x = [-2, -1, 0, 1, 2]
y = [99.98, 99.99, 100, 100.01, 100.02]
인과관계 x 상관관계
상관관계가 반드시 인과관계로 연결되는 것은 아니다.
사이트에 머문 시간과 친구의 수라는 두 척도가 비례관계에 있으나, 사용자는 사이트에 머문 시간이 많기 때문에 자연히 친구의 수가 늘어났을 수도 있고, 소통할 친구의 수가 많기 때문에 사이트에 오래 머무르는 것일 수도 있다.
혹은 둘 다 아닐 가능성도 있다!
인과관계를 확인해 보기 위해서는 데이터 값을 무작위로 선택해 확인해 보는 방법이 있다.
성질과 환경이 비슷한 두 그룹으로 사용자를 나누고 한 그룹에만 다른 요인을 적용시켜 인과관계를 확인할 수 있다.
예를 들어 ‘무작위로 일부 사용자를 선별, 각 사용자에게 일부 친구들의 글만 보여준다.’ 라는 요인이 사용자가 더 적은 시간을 보낸다는 결과를 낳는다면 친구 수의 증가에 따라 사이트 체류 시간이 증가한다는 가설이 어느 정도 맞다고 할 수 있다.